Temario de calculo - Reglas Para Calcular La Derivada


Temario de calculo

unidad I

Reglas Para Calcular La Derivada

Reglas generales de diferenciación

Linealidad

$left({f + g}right)' = f' + g'$

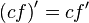
$left({cf}right)' = cf'$

Regla del producto

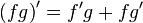
$left({fg}right)' = f'g + fg'$

Regla de la función recíproca

$left(frac{1}{f}right)' = frac{-f'}{f^2}$

Regla del cociente

$left({f over g}right)' = {f'g - fg' over g^2}, qquad g ne 0$

Regla de la cadena

$(f circ g)' = (f' circ g)g'$

Derivadas de funciones simples

${d over dx} c = 0$

${d over dx} x = 1$

${d over dx} (cx) = c$

${d over dx} x^c = cx^{c-1} qquad mbox{donde } x^c mbox{ y } cx^{c-1} mbox { se encuentran definidos}$

${d over dx} (cx^n) = cnx^{n-1}$

${d over dx} |x| = {|x| over x} = sgn x,qquad x ne 0$

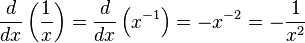
${d over dx} left({1 over x}right) = {d over dx} left(x^{-1}right) = -x^{-2} = -{1 over x^2}$

${d over dx} left({1 over x^c}right) = {d over dx} left(x^{-c}right) = -cx^{-c-1} = -{c over x^{c+1}}$

${d over dx}(sqrt[n]{x}) = { 1 over n sqrt[n]{x^{n-1}} }, mbox{sea }x > 0$

${d over dx} sqrt{x} = {d over dx} x^{1over 2} = {1 over 2} x^{-{1over 2}} = {1 over 2 sqrt{x}}, qquad x > 0$

${d over dx} f(x)^n = nf(x)^{n-1} cdot {d over dx}f(x)$

Derivada de la función inversa

$(f^{-1})' =frac{1}{f' circ f^{-1}}$ ,

para alguna función diferenciable f de un argumento real y con valores reales, cuando las composiciones indicadas e inversas existen.

Derivadas de funciones exponenciales y funciones logarítmicas

${d over dx} c^x = {c^x ln c },qquad c > 0$

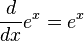
${d over dx} e^x = e^x$

${d over dx} log_c x = {1 over x ln c} qquad, c > 0, c ne 1$

${d over dx} ln x = {1 over x} qquad, x > 0$

${d over dx} ln |x| = {1 over x}$

${d over dx} x^x = x^x(1+ln x)$

$(f^g)'=f^g left( g'ln f + frac{g}{f} f' right)$

Derivada de la función potencial exponencial

${d over dx} f(x)^{g(x)} = f(x)^{g(x)}left({d over dx}f(x) cdot {g(x) over f(x)} + {d over dx}g(x) cdot ln f(x)right),qquad f(x) > 0$

Derivadas de funciones trigonométricas

Para más detalles sobre este tema, véase Derivación de funciones trigonométricas.

${d over dx},operatorname{sen},x = cos x$

${d over dx} cos x = -operatorname{sen},x$

${d over dx} tan x = sec^2 x = { 1 over cos^2 x} = 1+ tan^2x$

${d over dx} sec x = sec x tan x$

${d over dx} csc x = -csc x cot x$

${d over dx} cot x = -csc^2 x = { -1 over operatorname{sen}^2,x}$

${d over dx},operatorname{arcsen},x = { 1 over sqrt{1 - x^2}}$

${d over dx} arccos x = {-1 over sqrt{1 - x^2}}$

${d over dx} arctan x = { 1 over 1 + x^2}$

${d over dx} arcsec x = { 1 over xsqrt{x^2 - 1}}$

${d over dx} arccsc x = {-1 over xsqrt{x^2 - 1}}$

${d over dx} arccot x = {-1 over 1 + x^2}$

Derivadas de funciones hiperbólicas

${d over dx},operatorname{senh},x = cosh x = frac{e^x + e^{-x}}{2}$

${d over dx} cosh x = operatorname{senh},x = frac{e^x - e^{-x}}{2}$

${d over dx} tanh x = operatorname{sech}^2,x$

${d over dx},operatorname{sech},x = - tanh x,operatorname{sech},x$

${d over dx},operatorname{csch},x = -,operatorname{coth},x,operatorname{csch},x$

${d over dx},operatorname{coth},x = -,operatorname{csch}^2,x$

${d over dx},operatorname{arcsenh},x = { 1 over sqrt{x^2 + 1}}$

${d over dx},operatorname{arccosh},x = { 1 over sqrt{x^2 - 1}}$

${d over dx},operatorname{arctanh},x = { 1 over 1 - x^2}$

${d over dx},operatorname{arcsech},x = {-1 over |x|sqrt{1 - x^2}}$

${d over dx},operatorname{arccsch},x = {-1 over |x|sqrt{1 + x^2}}$

${d over dx},operatorname{arccoth},x = -{ 1 over x^2 - 1}$


	Temario de calculo

Este sitio web fue creado de forma gratuita con PaginaWebGratis.es. ¿Quieres también tu sitio web propio?

Registrarse gratis