Simetría
Las relaciones en inecuaciones pueden ser invertidas, queriendo decir esto que:
Para dos números reales, a y b:
Transitiva
Para tres números reales, a, b, y c:
- Si
 y
y 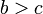 entonces
entonces 
- Si
 y
y  entonces
entonces 
- Si
 y
y  entonces
entonces 
Adición y sustracción
Las propiedades relacionadas con la adición y la sustracción:
Multiplicación y división
Las propiedades relativas a la multiplicación y la división:
Nota:
Si ambos términos de una inecuación se multiplican o dividen por la misma expresión negativa, el símbolo de la desigualdad se da la vuelta.
Aplicando una función a ambos miembros
Puede aplicarse cualquier función monótona creciente a ambos lados de una inecuación manteniendo el mismo signo de desigualdad.
Notación encadenada
La notación a < b < c establece que a < b (a menor que b) y que b < c (b menor que c) y aplicando la propiedad transitiva anteriormente citada, puede deducirse que a < c (a menor que c). Obviamente, aplicando las leyes anteriores, puede sumarse o restarse el mismo número a los tres términos, así como multiplicarlos o dividirlos todos por el mismo número (distinto de cero) invirtiendo las inecuaciones según su signo. Debe tenerse cuidado de utilizar en todos los casos el mismo número. Así, a < b + e < c es equivalente a a - e < b < c - e.
Esta notación se puede extender a cualquier número de términos: por ejemplo, a1 ≤ a2 ≤ ... ≤ an establece que ai ≤ ai+1 para i = 1, 2, ..., n−1. Según la propiedad de la transitividad, esta condición es equivalente a ai ≤ aj para cualquier 1 ≤ i ≤ j ≤ n.
Ocasionalmente, la notación encadenada se usa con inecuaciones en diferentes direcciones. En ese caso el significado es la conjunción lógica de las desigualdades entre los términos adyacentes. Por ejemplo, a < b > c ≤ d significa que a < b, b > c, y c ≤ d. Aparte del uso poco frecuente en matemáticas, esta notación existe en unos pocos lenguajes de programación tales como Python.
Desigualdades conocidas
Los matemáticos suelen usar inecuaciones para aproximarse a cantidades cuyas fórmulas exactas no pueden ser fácilmente computadas. Algunas se usan tan a menudo que se les ha puesto nombre, como:
-
Desigualdad de Azuma
-
Desigualdad de Bernoulli
-
Desigualdad de Boole
-
Desigualdad de Cauchy-Schwarz
-
Desigualdad de Chebyshov
-
Desigualdad de Chernoff
-
Desigualdad de Cramér-Rao
-
Desigualdad de Hoeffding
-
Desigualdad de Hölder
-
Desigualdad de las medias aritmética y geométrica
-
Desigualdad de Jensen
-
Desigualdad de Márkov
-
Desigualdad de Minkowski
-
Desigualdad de Nesbitt
-
Desigualdad de Pedoe
-
Desigualdad de Shapiro
-
Desigualdad triangular