Fracción parcial

El método de las fracciones parciales consiste en reducir un cociente de polinomios en fracciones más simples, que permitan obtener de manera inmediata una integral o una transformada de Laplace inversa (dos de sus aplicaciones). El requisito más importante es que el grado del polinomio del denominador sea estrictamente mayor que el grado del numerador. Para mayor claridad, sea:

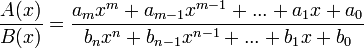
$frac{A(x)}{B(x)}= frac{a_mx^m+a_{m-1}x^{m-1}+...+a_1x+a_0}{b_nx^n+b_{n-1}x^{n-1}+...+b_1x+b_0}$

en donde: $m < n$ . Para reducir la expresión a fracciones parciales se deben seguir los siguientes pasos:

1) $B (x)$ se debe expresar de la forma:

B (x) = (x + a n)(x + a n - 1)...(x + a 1)(x + a 0)

B (x) = (a n x 2 + b n x + c n)(a n - 1 x 2 + b n - 1 x + c n - 1)...(a 1 x 2 + b 1 x + c 1)(a 0 x 2 + b 0 x + c 0)

Los cuatro casos posibles

es decir como el producto de factores lineales o cuadráticos. Al hacer esto la expresión se puede expandir de acuerdo a estos 5 casos:

a) factores lineales distintos:

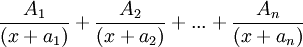
$frac{A_1}{(x+a_1)} + frac{A_2}{(x+a_2)} + ... + frac{A_n}{(x+a_n)}$

b) factores lineales repetidos:

$frac{A_1}{(x+a_1)} + frac{A_2}{(x+a_1)^2} + ... + frac{A_n}{(x+a_1)^n}$

c) factores cuadráticos distintos:

$frac{A_1 x +B_1}{(a_1 x^2+b_1 x+c_1)} + frac{A_2 x +B_2}{(a_2 x^2+b_2 x+c_2)} + ... + frac{A_n x +B_n}{(a_n x^2+b_n x+c_n)}$

d) factores cuadráticos repetidos:

$frac{A_1 x +B_1}{(a_1 x^2+b_1 x+c_1)} + frac{A_2 x +B_2}{(a_1 x^2+b_1 x+c_1)^2} + ... + frac{A_n x +B_n}{(a_1 x^2+b_1 x+c_1)^n}$

e) Una mezcla de todos los anteriores

Cómputo de las constantes

Para hallar las constantes, en el caso a) se puede utilizar la siguiente fórmula:

$A_k=left[frac{A(x)}{B(x)}(x+a_k)right]_{x=-a_k}$ en donde k=1,2,...,n

Para los otros casos no existe una formulación específica. Sin embargo estos se pueden resolver simplificando y formando un sistema de ecuaciones con cada una de las Ak, se resuelve el sistema y se obtienen los valores de los Ak