Temario de calculo - Limites De Funciones Trascendentes Y Algebraicas

Función trascendente

Una función trascendente es una función que no puede ser representada por una ecuación polinómica cuyos coeficientes son a su vez polinomios, en comparación una función algebraica sí satisface tal tipo de ecuación. Es decir una función de una variable es trascendente si es independiente en un sentido algebraico de dicha variable.

Funciones algebraicas y trascendentes

El logaritmo y la función exponencial son ejemplos de funciones trascendentes. El término función trascendente a menudo es utilizado para describir a las funciones trigonométricas, o sea, seno, coseno, tangente, cotangente, secante, y cosecante.

Una función que no es trascendente se dice que es algebraica. Ejemplos de funciones algebraicas son las funciones racionales y la función raíz cuadrada.

La operación de calcular la función primitiva (o integral indefinida) de una función algebraica es una fuente de funciones trascendentes. Por ejemplo, la función logaritmo surgió a partir de la función recíproca en un intento para calcular el área de un sector hiperbólico. Por lo tanto el ángulo hiperbólico y las funciones hiperbólicas senh, cosh, y tanh son todas funciones trascendentes.

Función algebraica

En matemáticas, una función algebraica es una función que satisface una ecuación polinómica cuyos coeficientes son a su vez polinomios. Por ejemplo, una función algebraica de una variable x es una solución y a la ecuación

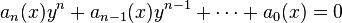
$a_n(x)y^n+a_{n-1}(x)y^{n-1}+cdots+a_0(x)=0$

donde los coeficientes a_i(x) son funciones polinómicas de x. Una función que no es algebraica es denominada una función trascendente.

En términos más precisos, una función algebraica puede no ser estrictamente una función, por lo menos no en el sentido convencional. Por ejemplo sea la ecuación de una circunferencia:

$y^2+x^2=1.,$

La misma determina y, excepto por su signo:

$y=pm sqrt{1-x^2}.,$

Sin embargo, se considera que ambas ramas pertenecen a la "función" determinada por la ecuación polinómica.

Una función algebraica de n variables es definida en forma similar a la función y que es solución de la ecuación polinómica en n + 1 variables:

$p(y,x_1,x_2,dots,x_n)=0.,$

Normalmente se supone que p debe ser un polinomio irreducible. La existencia de una función algebraica es asegurada por el teorema de la función implícita.

Formalmente, una función algebraica de n variables en el cuerpo K es un elemento del cierre algebraico del cuerpo de las funciones racionales K(x₁,...,x_n). Para poder comprender a las funciones algebraicas como funciones, es necesario incorporar ideas relativas a las superficies de Riemann o en un ámbito más general sobre variedades algebraicas, y teoría de haces.